PART 자료구조 Contents

Chapter 01 숫자

인간 : 10개의 손가락으로 나타내는 10진법이 자연스러움

컴퓨터 : 전자 상태 신호인 참, 거짓을 주고 받는 이진법(binary)표현이 더 적합.

컴퓨터는 정보를 비트(bit)로 표현. 또한 8진법과 16진법 등 2의 배수 표현도 사용

파이썬에서 정수: int, 불변immutable형.

파이썬 정수 크기

(정수).bit_length() : 정수를 나타내는데 필요한 바이트 수를 확인(파이썬 3.1 이상)

>>> (999).bit_length()
10

int(문자열, 밑) : 어떤 문자열을 정수로 변환casting하거나 다른 진법의 문자열을 정수(10진법)으로 변환

>>> s = '11'
>>> d = int(s)
>>> print(d)
11
>>> b = int(s, 2)
>>> print(b)
3

int메서드의 밑은 2에서 36사이의 선택적 인수(optional argument)

문자열 s에서 밑 범위의 숫자를 벗어나는 값을 입력한다면 int 메서드에서 ValueError예외가 발생한다.

예를 들어 s = '12' 에 대해 실행하면 예외가 발생한다.

IEEE 754: 전기 전자 기술자 협회(IEEE)에서 개발한, 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준

파이썬에서 부동소수점은 float으로 나타내며 불변형

단정도(single precision)방식에서 32비트 부동소수점을 나타낼 때 1비트는 부호sign(0: 양수, 1: 음수), 23비트는 유효 숫자 자릿수significant digits(혹은 가수mantissa), 8비트는 지수exponent다.

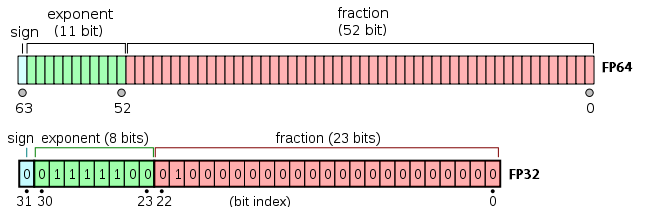
float

example: -118.625₁₀를 32비트 단정도로 표현해보면?

숫자의 절댓값을 이진수로 변환
부호sign는 음수이므로 1

->: $1110110.101$₍₂₎
변환 된 이진수 정규화(소수점 왼쪽 이동시켜 1만 남게 함)

->: $1.110110101$₍₂₎ * $2^6$
위 숫자를 가수부(23비트)에 넣고 부족한 자릿수는 0으로 채움

->: $11011010100000000000000$
지수 6에 바이어스^bias 127(0111 1111₍₂₎) 더함

6₍₁₀₎ + 127₍₁₀₎ = 133₍₁₀₎ = 10000101₍₂₎

(bias는 2^k-1 로 주어지는데 k는 지수부의 비트수 8이다. 즉 2⁷)

-»: 1(부호)10000101(지수, 8자리)11011010100000000000000(가수, 23자리)

배정도^{double precision}방식

이진수 분수^{binary fraction}로 표현되기 때문에 함부로 비교하거나 빼면 안됨.

2진수는 대개 10진법으로 정확하게 표현 가능하지만 2진법으로 표현하기 어려운 숫자도 있다.

예: 0.1₍₁₀₎ = 0.00110011001100…₍₂₎

>>> 0.2 * == 0.6
False
>>> 1.2 - 0.2 == 1.0
True
>>> 0.1 * 0.1 == 0.01
False

고정소수점 방식은 정확도는 높지만 큰 수를 표현하려면 많은 메모리가 사용된다.

부동소수점 방식은 이 문제를 해결하기 위해 도입되었음.

가장 좋은 건 float을 사용하여 비교하지 않는게 좋다.

정수를 처리하는데 드는 비용보다 실수를 처리하는데 드는 비용이 압도적으로 많기 때문.

속도가 중요하다면 정수를 사용하는 것이 좋다.

대신 동등성 테스트^{equality test}는 사전에 정의된 정밀도 범위 내에서 수행되어야 한다.

예를 들어 unittest 모듈의 assertAlmostEqual() 메서드 같은 접근법을 사용하는 방법이 있다.

>>> def a(x, y places=7):
...    return round(abs(x-y), places) == 0

또한 부동소수점의 숫자는 메모리에서 비트 패턴으로 비교할 수 있다.

>>> round(112.459, -1)
110.0
>>> round(112.459, 2)
112.46